Purpose
We
had to calculate the period of an isosceles triangle where the pivot is at the
base and on its top point and compare it to our experimental value
Procedure
 |
| The set up at the top point of the isosceles triangle |
- logger pro + photogate
- styrofoam cut out of an isosceles triangle
- first we had to calculate what the theoretical value of the period would be for both cases
- we had to calculate for the center of mass for the isosceles triangle
- then logger pro and the photo-gate were set up
- the pivot is then placed at one of the locations (centered base or the top point) of the isosceles triangle
- the period is measured
Data
isosceles triangle measurements
- base: 0.10 m
- height: 0.14 m
 | |
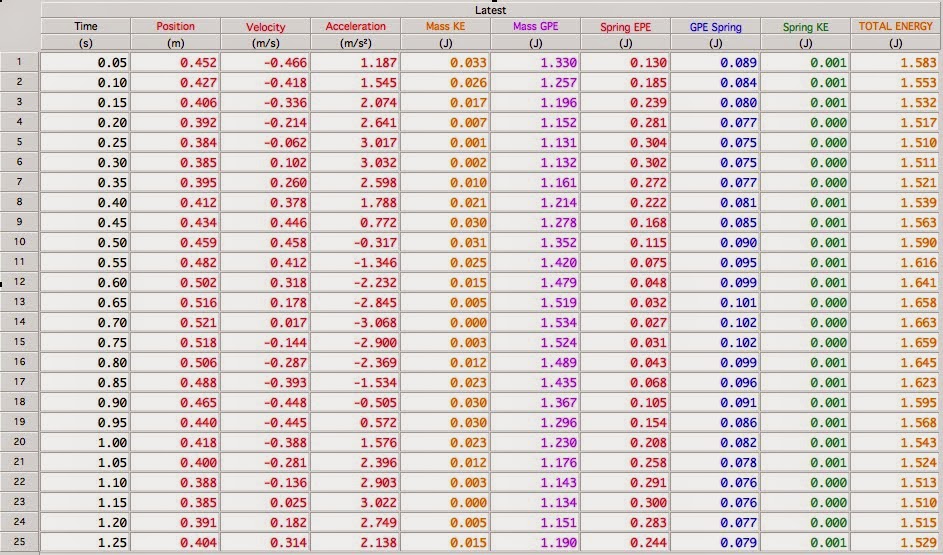
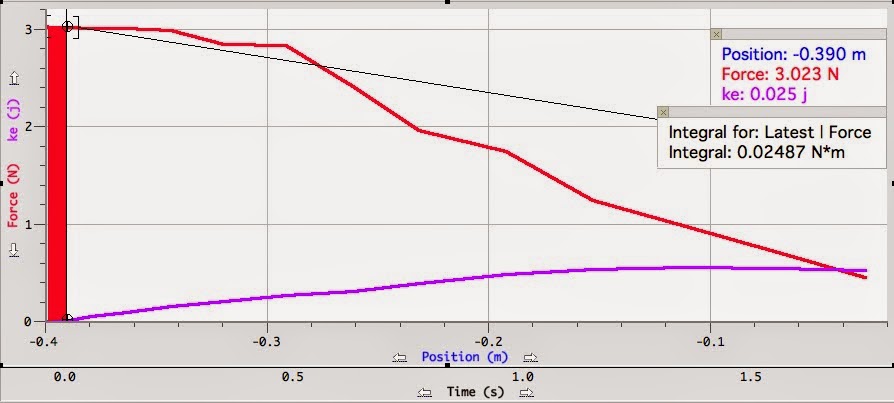
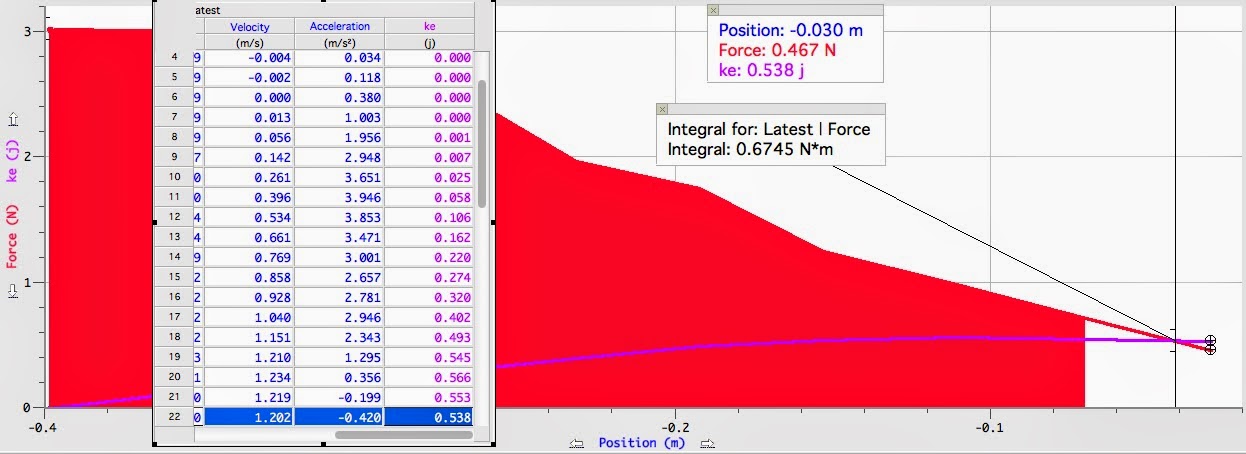
| This is the period for the isosceles triangle at its base: 0.664. The period for the isosceles triangle at its top point is 0.591 |
Data Analysis / Calculations
 | ||
| This is the calculations for the center of mass for the isosceles triangle in the y-direction |
 | ||||
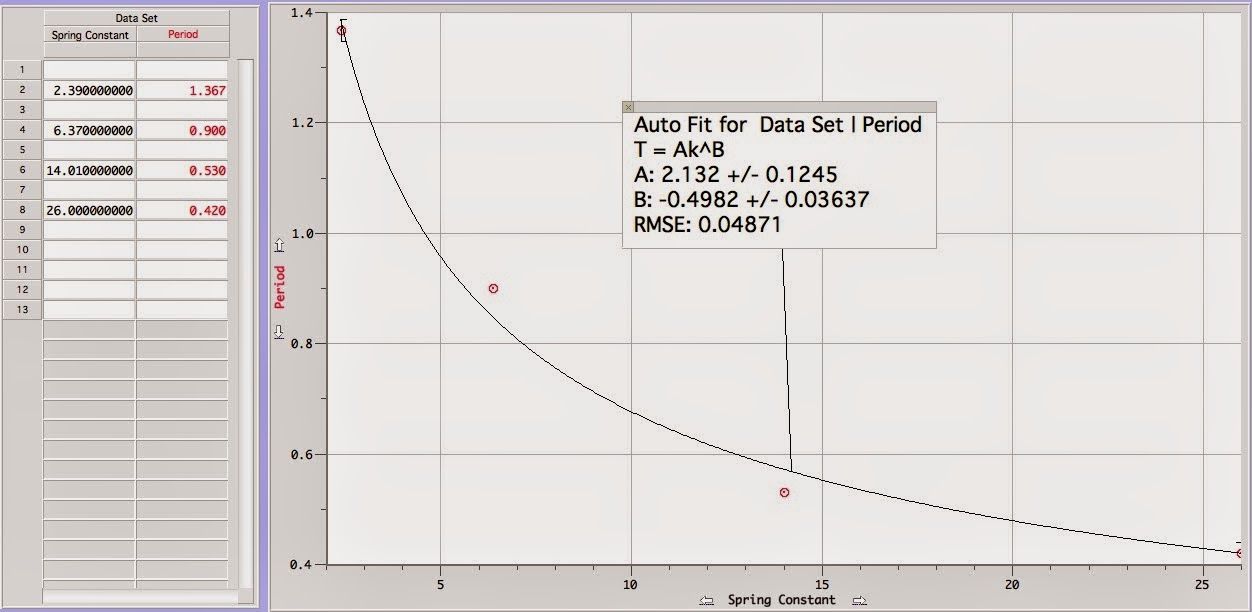
| This is the calculations for the periods of the isosceles triangle based on where the pivot is |
Summary
In this lab we aimed to find the period of an isosceles triangle at its top point and at its center base. We found the theoretical value of the period and then did the experiment.
When it was at its base, the theoretical value was 0.664 while the calculated value was 0.664, so that was a success.
When it was at its top point, the theoretical value was 0.591 while the calculated value was 0.564, so there was about a 4% error, when we were supposed to get within 1%.




























%2B10.13.tiff)