Purpose
In this lab, we used an inertial balance and a photo-gate to help us find a relationship between mass(m+M tray) and a period(T) by measuring the period of different masses. The equation: T = A (m+Mtray)^n is used to help with seeing the relationship.
 |
| Lab Equipment: Inertial Balance (red device on left) held by C-clamp. Photo-gate (black device on right). |
Experiment / Data
As the inertial balance passed between the photo-gate, using LabPro, the period of the balance was recorded for a time of 5 seconds. This was done with masses of 0 grams to 800 grams in increments of 100 grams. We also recorded the period and mass of 3 "unknowns" to see if the mass could later be determined by formula.
 |
Data Table: Mass (g) and measured periods per 5 seconds
|
 |
| Data Table 2: This table shows the mass and period of 3 "unknowns" |
The formula: T=A(m+Mtray)^n was then manipulated it to be lnT = n
ln(m+Mtray) + lnA so in order to resemble y = mx + b. With that and the
data collected, a graph was created with an x axis of lnT and y
axis of ln(m+Mtray), where T represents the period and (m+Mtray)
represent the mass of the inertial balance tray along with the mass added.
Using the data the graph provided, a line of best fit helped in
determining the mass of the inertial balance tray itself, which then in
helping finding the mass of the "unknowns."
 |
| This number is the mass of the tray, and what helped determine the line of best fit |
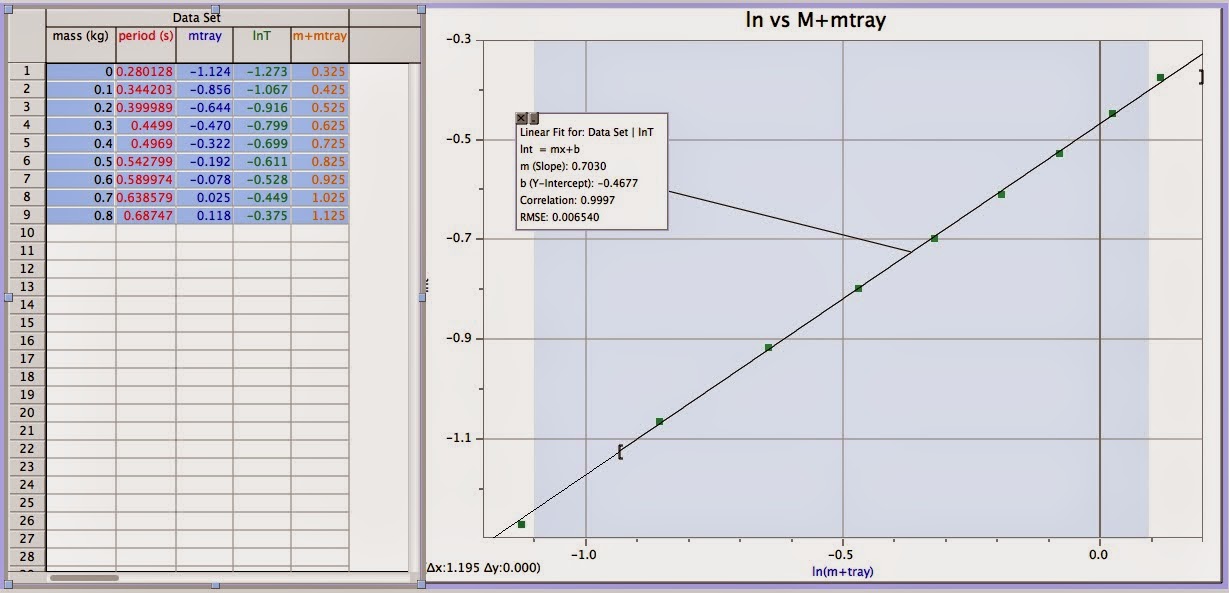 |
| This graph shows the relationship between the mass and period, ln(m+Mtray) vs lnT |
 |
| This is the data the graph presents. The correlation is 0.9997, which means that there is a linear relationship: as mass increases, so does the period. |
Calculations
Given the data from the graph, it's then possible to find the values of A and n. With those two values, then the value for T can be calculated and compared to a recorded value of T. In the calculations, the value of the compared T is 0.280128 with a mass of 0 grams.
 |
| Calculations: The value of n is already known and through calculations, the value for A is found. With these two values, the value of T is found when the mass is 0 grams and then compared to the recorded value. The numbers are close and present a percent error of less than 5%, meaning that the mass of the tray is an acceptable value. |
|
|
With the values of A and n, the values of mass of the three "unknowns" can then be calculated. After each mass of the "unknowns" are calculated, they are then compared to the measured mass found from using the balance.
 |
| Unknown #1 |
 |
| Unknown #2 |
 |
| Unknown #3 |
 |
| Measured masses and calculated masses of the 3 "unknowns" |
Summary
In this lab, a relationship between mass and period was found using an inertial balance and a photo-gate. The photo-gate was used to measure the periods of each mass that was on the inertial balance, starting from 0 grams and increasing 100 grams until 800 grams was reached. With the data, a graph was able to help find the relationship between mass and period. The graph shows a linear relationship, which is that as the mass increases, so does the period.
Using the formula: T = A (m+Mtray)^n and the data from the graph the values of A and n were found. Once those values were found, then it was possible to go back and calculate the period(T) and compare it the measure period(T). The values also allowed for the mass of 3 "unknown" objects to be calculated and compared to the measured masses. When comparing the period and masses with the calculated and compared, the differences between them were less 10%.











